
Les Sangaku sont des tablettes votives offertes dans des sanctuaires shinto (et parfois dans des temples boudhistes) au Japon. Les problèmes figurant sur les sangaku sont typiques des mathématiques japonaises et utilisent souvent de nombreux cercles ce qui est inhabituel dans les mathématiques occidentales. Ces problémes peuvent souvent être vu comme des jeux mathématiques (comme les Sudoku Japonais)...
On trouve des exemples de ces problèmes dans les pages Typical Sangaku Problems et San Gaku : Japanese Temple Geometry Problems qui sont malheureusement en anglais.

Exemple de problème :
Trouver une relation entre les rayons de ces trois cercles tangents entre eux et à une même droite.

Pour ceux qui se sentiraient intéressés par ces problèmes, Géry Huvent vient de publier aux éditions Dunod le livre "Sangaku : Le mystère des énigmes géométriques japonaises".
Présentation du livre :
"A travers une sélection des plus beaux et plus intéressants sangaku, classés par difficulté et présentés avec leur solution complète, cet ouvrage vous fera découvrir ce joyau encore mal connu des mathématiques japonaises."
On peut commander ce livre sur amazon...
Lien permanent | Lien relatif

Le Tournoi des Villes est un tournoi mathématique pour les élèves de la quatrième à la terminale qui a démarré en Russie en 1980 et est devenu réellement international depuis.
Il aura lieu cette année les dimanches 23 novembre 2008 et 8 mars 2009 à 9h à Paris et à Lyon.
Il faut s'inscrire sur le site qui précise les modalités du concours (épreuves de 4 ou 5 heures) et propose des archives complètes et intéressantes, pour s'entrainer, mais aussi pour tous ceux qui aiment chercher.
Exemple d'exercice (niveau première-terminale) :
Une suite de 0 et de 1 est construite selon la règle suivante : le k-ième terme de la suite est un 0 si la somme des chiffres de k est paire et un 1 si elle est impaire.
Le début de cette suite est donc : 101010101101010101001....
Montrer que cette suite n’est pas périodique.
Lien permanent | Lien relatif

La galerie Cecconi a changé d'adresse et a fait peau neuve.
On y trouve de nouveaux dessins et, bien sûr, une nouvelle énigme illustrée.
...
Lien permanent | Lien relatif

Le site Diophante met en ligne chaque mois :
- les problèmes du mois
- un casse-tête
- des problèmes ouverts
Ce mois-ci, trois ans et demi après son lancement, le site Diophante a doublé de volume et met désormais à la disposition des internautes plus de 800 problèmes et récréations mathématiques.
Pour le mois d'octobre, sont proposés les problèmes aux doux titres suivants :
Concaténations en tous genres, Fermat à un chouia près, Ne pas s'emballer...dans les emballages,
Retour à la fourmilière, Non fiat lux, Pour le plaisir des macarons de Montmorillon.
Voici Retour à la fourmillière :
Après une journée laborieuse, la fourmi rousse et la fourmi noire prennent le chemin du retour, chacune en direction de sa fourmilière. Leurs deux trajectoires sont rectilignes et à tout instant chaque fourmi garde sa vitesse et sa direction. A un certain moment, elles sont à une distance d > 0 l'une de l'autre, 17 secondes plus tard, cette distance est de 87 cm. 18 autres secondes après, cette distance est ramenée à 75 cm. Encore 70 secondes après, elles sont à 65 cm l'une de l'autre. Vont-elles se rencontrer ? Si oui, à quel moment ? Si non, quelle est la plus courte distance qui les séparera ou les a séparées ?
Lien permanent | Lien relatif

Le mathématicien flamand Adriaan van Roomen, francisé en Adrien Romain, latinisé en Adrianus Romanus est né le 29 septembre 1561.
Il s'est intéressé au calcul de pi et des tables trigonométriques.
Dans son premier ouvrage scientifique intitulé «Ideae mathematicae primasive methodus polygonorum» paru à Anvers en 1593, il est le premier à faire un emploi systématique de notations abrégées comme sin(A + B).
C'est aussi dans ce livre qu'il défie les mathématiciens de son temps de résoudre une équation du 45e degré :
45x - 3795x3 + 95634x5 - 1138500x7 + 7811375x9 - 34512075x11 + 105306075x13 - 232676280x15 + 384942375x17 - 488494125x19 + 483841800x21 - 378658800x23 + 236030652x25 - 117679100x27 + 46955700x29 - 14945040x31 + 3764565x33 - 740259x35 + 111150x37 - 12300x39 + 945x41 - 45x43 + x45 = C , avec
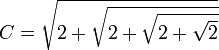
Le mathématicien français François Viète fut le premier à résoudre cette énigme.
Lien permanent | Lien relatif

Le mathématicien Hans Freudenthal est né le 17 septembre 1905.
Il a oeuvré pour l'ouverture de l'enseignement des mathématiques "pour tous". Une médaille lui doit son nom : la médaille Hans-Freudenthal récompense un ensemble de travaux de recherche en didactique des mathématiques d'intérêt majeur sur un thème précis."
On trouve sur le site )i(interstices, une page présentant l'incroyable problème de Freudentahl où savoir qu'un autre ne sait pas peut nous aider à savoir !
Enoncé
On choisit deux entiers X et Y, avec 1<X<Y et X+Y<=100. On indique à Patricia le produit P de X et Y. On indique à Sylvie la somme S de X et Y.
Le dialogue est alors le suivant :
1. Patricia : « Je ne sais pas quels sont les nombres X et Y. »
2. Sylvie : « Je savais que vous ne connaissiez pas X et Y. »
3. Patricia : « Eh bien alors, maintenant, je connais X et Y. »
4. Sylvie : « Eh bien, moi aussi je les connais maintenant. »
À vous de trouver X et Y.
Lien permanent | Lien relatif

Naufragé des airs sur l'Ile mystérieuse (Partie 1, chapitre 14) de Jules Verne, l'ingénieur Cyrus Smith veut mesurer la hauteur d'une falaise.
Saurez-vous l'aider à terminer son calcul ?
Cyrus Smith s'était muni d'une sorte de perche droite, longue d'une douzaine de pieds, qu'il avait mesurée aussi exactement que possible, en la comparant à sa propre taille, dont il connaissait la hauteur à une ligne près. Harbert portait un fil à plomb que lui avait remis Cyrus Smith, c'est-à-dire une simple pierre fixée au bout d'une fibre flexible.
Arrivé à une vingtaine de pieds de la lisière de la grève, et à cinq cents pieds environ de la muraille de granit, qui se dressait perpendiculairement, Cyrus Smith enfonça la perche de deux pieds dans le sable, et, en la calant avec soin, il parvint, au moyen du fil à plomb, à la dresser perpendiculairement au plan de l'horizon.
Cela fait, il se recula de la distance nécessaire pour que, étant couché sur le sable, le rayon visuel, parti de son oeil, effleurât à la fois et l'extrémité de la perche et la crête de la muraille. Puis il marqua soigneusement ce point avec un piquet.
Alors, s'adressant à Harbert :
- Tu connais les premiers principes de la géométrie ? lui demanda-t-il.
- Un peu, monsieur Cyrus, répondit Harbert, qui ne voulait pas trop s'avancer.
- Tu te rappelles bien quelles sont les propriétés de deux triangles semblables ?
- Oui, répondit Harbert. Leurs côtés homologues sont proportionnels.
- Eh bien, mon enfant, je viens de construire deux triangles semblables, tous deux rectangles : le premier, le plus petit, a pour côtés la perche perpendiculaire, la distance qui sépare le piquet du bas de la perche, et mon rayon visuel pour hypoténuse ; le second a pour côtés la muraille perpendiculaire, dont il s'agit de mesurer la hauteur, la distance qui sépare le piquet du bas de cette muraille, et mon rayon visuel formant également son hypoténuse, - qui se trouve être la prolongation de celle du premier triangle.
- Ah ! monsieur Cyrus, j'ai compris ! s'écria Harbert. De même que la distance du piquet à la perche est proportionnelle à la distance du piquet à la base de la muraille, de même la hauteur de la perche est proportionnelle à la hauteur de cette muraille.
- C'est cela même, Harbert, répondit l'ingénieur, et quand nous aurons mesuré les deux premières distances, connaissant la hauteur de la perche, nous n'aurons plus qu'un calcul de proportion à faire, ce qui nous donnera la hauteur de la muraille et nous évitera la peine de la mesurer directement. »
Les deux distances horizontales furent relevées, au moyen même de la perche, dont la longueur au-dessus du sable était exactement de dix pieds.
La première distance était de quinze pieds entre le piquet et le point où la perche était enfoncée dans le sable.
La deuxième distance, entre le piquet et la base de la muraille, était de cinq cents pieds.
Ces mesures terminées, Cyrus Smith et le jeune garçon revinrent aux Cheminées.
Lien permanent | Lien relatif

Le numéro 13 de la Feuille @ problèmes vient de sortir.
Il s'agit d'un numéro spécial vacances, avec pour thème : le problème dont vous êtes le héros ...
On y trouve aussi un problème de construction à solutions multiples :
"Vous trouverez sans difficulté une solution au problème suivant. Mais combien de solutions pouvez-vous imaginer ?
Construire un triangle, connaissant la mesure de ses angles et son périmètre."
Lien permanent | Lien relatif
Précédent Suivant




 Calendrier
Calendrier


